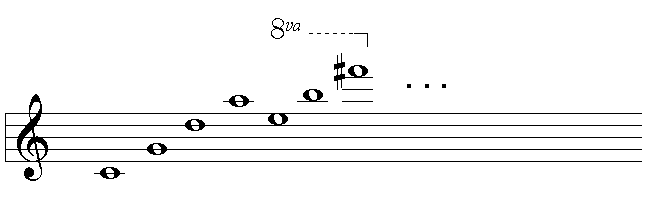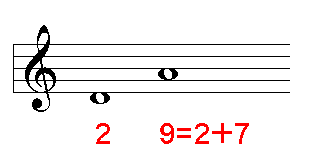ショパンのプレリュードから群論へ

不思議なタイトルのページで恐縮です.

1. 西洋音階の12の音と五度圏

バッハの「平均律クラヴィーア曲集」, ショパンの「24の前奏曲 Op.28」はいずれも24種類ある長音階, 短音階のすべてを1回ずつ使い, すべての調のための曲が1曲ずつ入っている曲集です. 調の配列はどうなっているかというと (長調だけ数えます), バッハの方はハ - 嬰ハ - ニ - 変ホ (=嬰ニ) - ... という具合に, 主音が半音ずつ上がって行ってすべての調をつくします.



半音ずつ上がって音階内のすべての音をつくす

しかしショパンの方は違った配列になっています. やはり長調だけ数えると, ハ - ト - ニ - イ - ホ - ロ - 嬰ヘ - ... という具合で, 主音が完全五度 (ドと, すぐ上のソの間の音程) ずつ上がって行ってすべての調をつくす, という仕組みになっています.



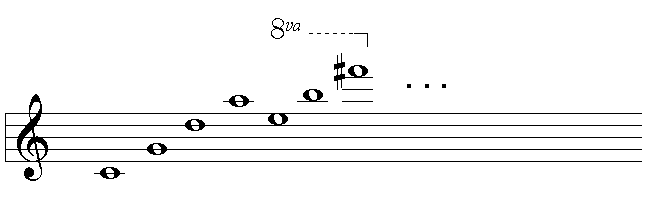
完全五度ずつ上がって行くと ...

　初めて見たときはこれが不思議で, 「本当に全部揃っているのかな」などと書き出してみたこともあったように思います. では, このような「音の上がり方」は他にあるでしょうか. また, それらに共通の特徴は何でしょうか.
　ピアノなどで試してみればすぐわかりますが,「ある音から出発して一定の音程だけ上げる操作を12回繰り返すと, 音階内の12の音すべてを一巡してもとの音に戻る」ような音程は, 次の4つです:

半音ずつ上がっていけばすべての音を1回ずつ通っていくのは当たり前, また「長7度上げる」は「半音下げる」と同じと見てよいわけですから, これも当たり前です. 自明でないのは完全4度と完全5度ということになります.
　ところで, 上記4つの音程が, それぞれいくつの半音でできているか見てみると となります. この 1, 5, 7, 11 という数が何であるかというと, ちょうど1 から 11 までの整数のうち, 12 と互いに素なもの全体ということになります. 2 つの整数 a, b が互いに素とは, a と b の最大公約数が 1 であることです. 音階内の音の総数 12 と互いに素であることが本質的役割を果たします.
　なお, 1 つの音から完全五度上の音を順次たどって行って, それらを円周上に並べたものは「五度圏」(circle of fifth) と呼ばれ, 音楽理論でよく使われています. 「五度圏」で検索すると詳しく解説したホームページがたくさん見つかります.

2. 合同式入門

本ホームページは数学コースのページですから, 最後はやはり数学へと持って行きます. 紙と鉛筆を用意して, 簡単な計算をやってみましょう.
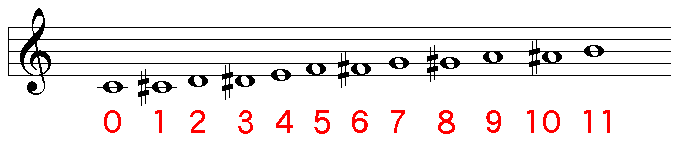
　まず次のように, 12 の音に 0 から 11 まで番号をつけます (1 から 12 でもいいですが, 数学としては 0 からの方が扱いやすいでしょう).


好きな音を 1 つ取り, その番号に 7 を足します. 足した結果の数はもとの音の完全五度上の音を表しているはずです.

(例) 2+7=9. 9 (イ) は 2 (ニ) の完全五度上の音.

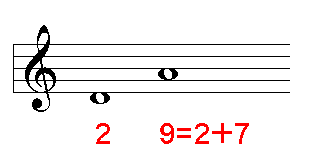
これを繰り返して行きますが, 足した結果はすぐに12以上の数になってしまいます. その場合は12を引いて, 11以下の数になるようにします. これはちょうど, 1 オクターヴ下の音に下げることと同じです.

(上の例の続き) 9+7=16, 16-12=4.

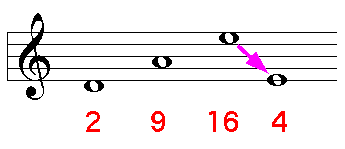
16 と 4 は同じホ音を表します. このことを数学記号を使って

16≡4 (mod 12)

と表しましょう(一般に整数 a, b, n に対して, a≡b (mod n) とは「a と b の差が n で割り切れる」という意味です. これを「合同式」といいます). 上の例をどんどん続けます. あらためて最初から書くと:

2+7=9
9+7=16≡4 (mod 12)
4+7=11
11+7=18≡6 (mod 12)
6+7=13≡1 (mod 12)
1+7=8
8+7=15≡3 (mod 12)
3+7=10
10+7=17≡5 (mod 12)
5+7=12≡0 (mod 12)
0+7=7
7+7=14≡2 (mod 12)

このように, 2, 9, 4, 11, 6, 1, 8, 3, 10, 5, 0, 7 と, 0 から 11 までのすべての数を過不足なく一巡し, 12 回目に確かにもとの 2 に戻ってきました (合同式の計算もこのくらいやると少しは慣れてくるでしょう).
　ここでは「完全五度上げる」に対応して, 7 を足していく計算を続けましたが, 「完全四度上げる」に対応して 5 を足していっても同様の結果となります (実際に確かめてみましょう).

3. ユークリッド互除法からの一定理

　音楽のことだけ考えるなら, 5 と 7 と 12 の関係だけが問題ですから, 上のように実際にやってみればもう終わりです. しかし, こうして現象として観察しても, 「なぜそうなるのか」がわかった気はしないですね. 多少なりともわかった気になるためには, もっと一般的な立場に立って考えてみなければなりません. それを可能にしてくれるところに数学の「ありがたみ」があると言ってもいいでしょう. 少し難しいですが, この現象を説明してくれるのは次の事実です:

定理. 互いに素な任意の整数 a, b に対して
am+bn=1
となる整数 m, n が必ず存在する.

これは専門的な数学でも随所で使われる有名で基本的な結果です. 証明にはそれほど高度な数学が必要というわけではないのですが, 2 つの整数の最大公約数を求める「ユークリッド互除法」の手順をきちんと数式で表す必要があり, それには幾分かの数学的修練が必要でしょう. 高校教科書でもそれほど厳密な証明が紹介されているわけではありません. 証明は「初等整数論」という分野を扱う本には大抵載っています (例えば, 河田敬義『数論』(岩波書店, 1992), p.11. 少し趣の違った証明として, 石田信『代数学入門』(実教出版, 1978), p.59-60 など).
　さて, 五度圏の話に戻ります. 完全五度上げる操作ばかりですべての音が現れる理由を上の定理をもとに探ってみましょう. それには,
完全五度上げる操作何回か ( m 回としましょう) の繰り返し (とオクターヴ下げることの組合わせ) で半音上げる操作が表せる
ことが言えればいいでしょう. なぜなら, 半音上げる操作の繰り返しですべての音程が得られるのは自明ですから, 上のことが言えれば結局 (オクターヴの差は無視すれば),

半音 k 個の音程 = k × (m × 完全五度上げる) = km × 完全五度上げる

となり, 任意の音程が (オクターヴの差を無視すれば) 完全五度の組合わせのみで表せることがわかります.
　そのために, 上の定理で a=7, b=12 の場合を考えます. すると「7m+12n=1 となる整数 m, n が存在する」, となります(こんな m, n の組は例えば m=7, n=-4. 他にも無限個あるはずです). この式で, まず 7m は「完全五度上げる操作を m 回繰り返す」( m<0 なら下げる操作) と読めます. すると次の 12n は「1 オクターヴ上げる操作を n 回繰り返す」( n<0 なら下げる)ことを表します. 右辺の 1 はもちろん半音の音程を表します. こう考えると, 7m+12n=1 は「完全五度 m 回の移動とオクターヴ n 回の移動で半音上げる操作が実現できる」ことを表すことになるのです.



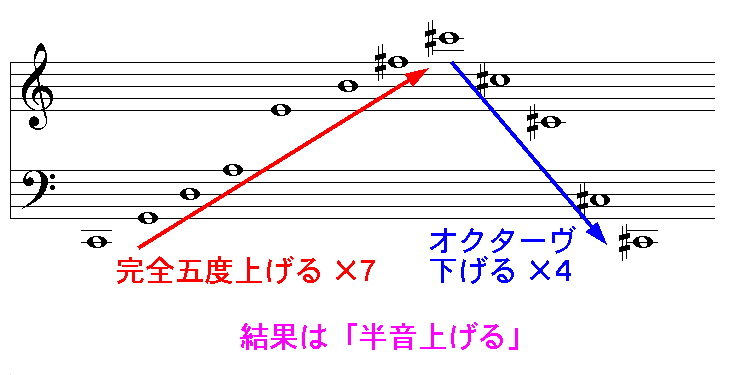
7×7+12×(-4)=1 の図


4. 合同式から群へ

　上の話, 簡単なようでなかなか難しいですね. それもそのはず, 大学で学ぶ「群論」の初歩が, 実は含まれているからです. 上でやったような, 0 から 11 までの整数の足し算を, 12 以上の数が現れないようにしながら行なうことで, 0 から 11 までの整数の集合に 1 つの「演算」が定義できたことになります. 12 に限らず, 一般に整数 n (>0) に対して 0 から n-1 までの整数の集合を考え, それらの数の間の足し算を, n 以上の数が現れないようにしながら行なう, という演算が定義できます.
　このようなものは「群」の一例で, 「整数の剰余類のなす群」といいます. 群は他にもいろいろあって, 数学のあらゆる場面に顔を出します. 数学の内部で重要であるばかりでなく, 実社会でも見えないところで使われています. その 1 つの例は「暗号」です. 「符号」と「暗号」は似ているようで実は少し違います. どちらもディジタル方式で情報をやりとりする場合に不可欠なものですが, 符号が情報を間違いなく伝えることを目標にしているのに対し, 暗号は情報を第三者に知られないよう伝えることを目標にしています. 暗号に使われている群は, 上の整数の剰余類のなす群に似た, もう少し難しい群です.
　合同式の計算は慣れれば簡単ですが, こういうことを出発点として, 実際に役立つ技術が生まれている, と聞けば, その先を勉強してみたくなりませんか ?

2007.4 公開, 2019.11 改訂

応用代数学研究室に戻る