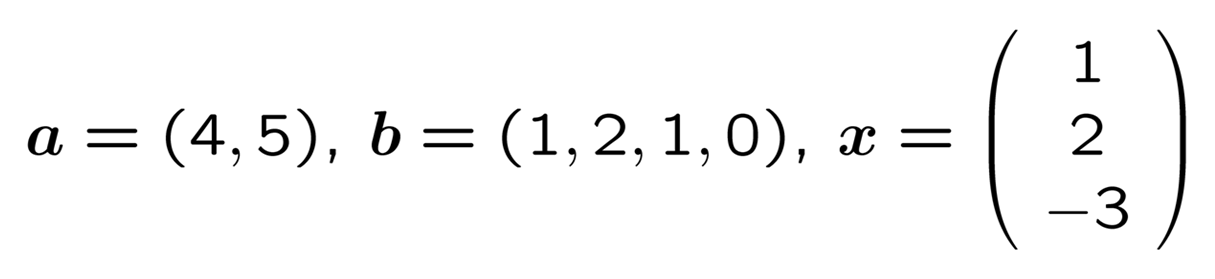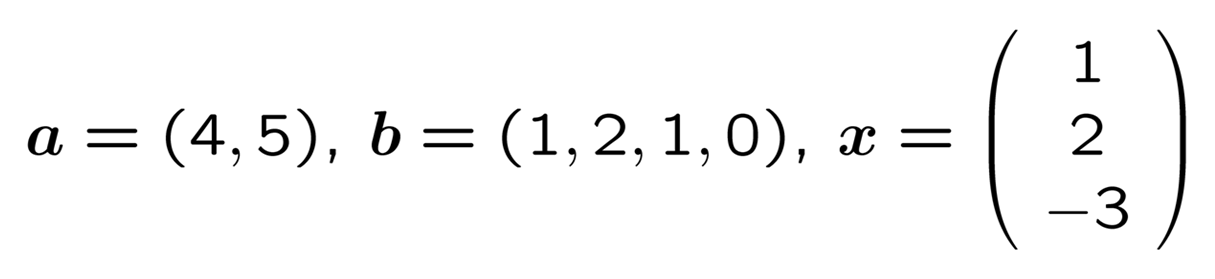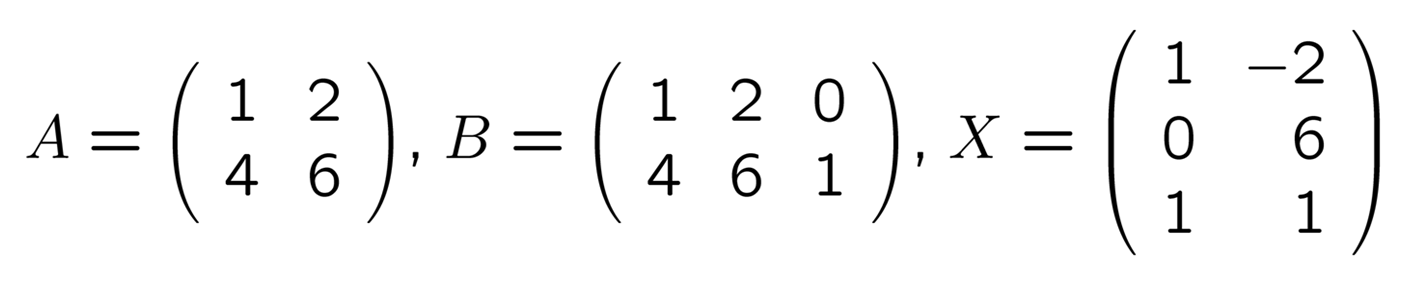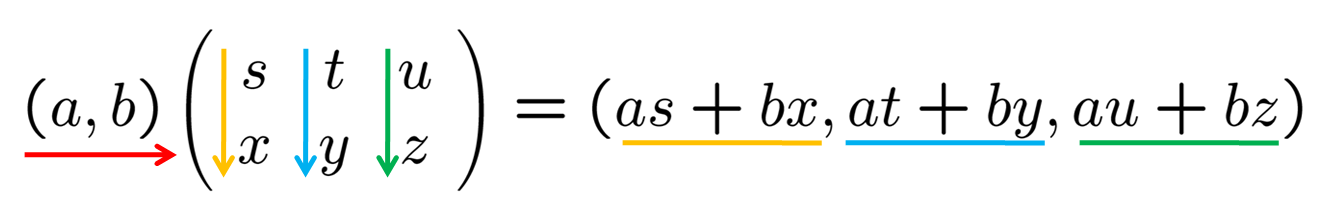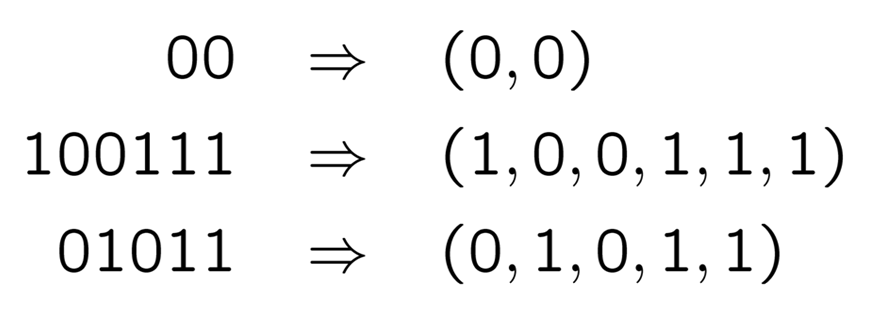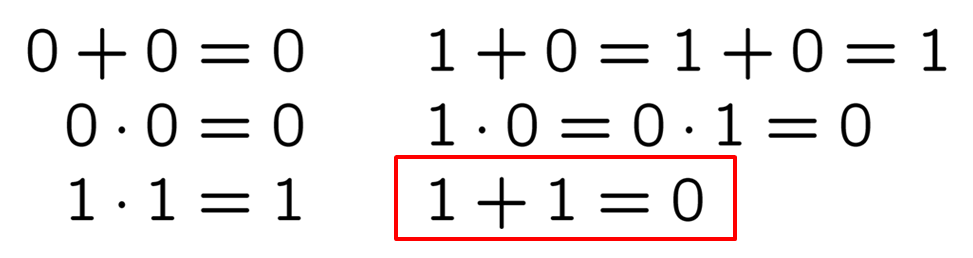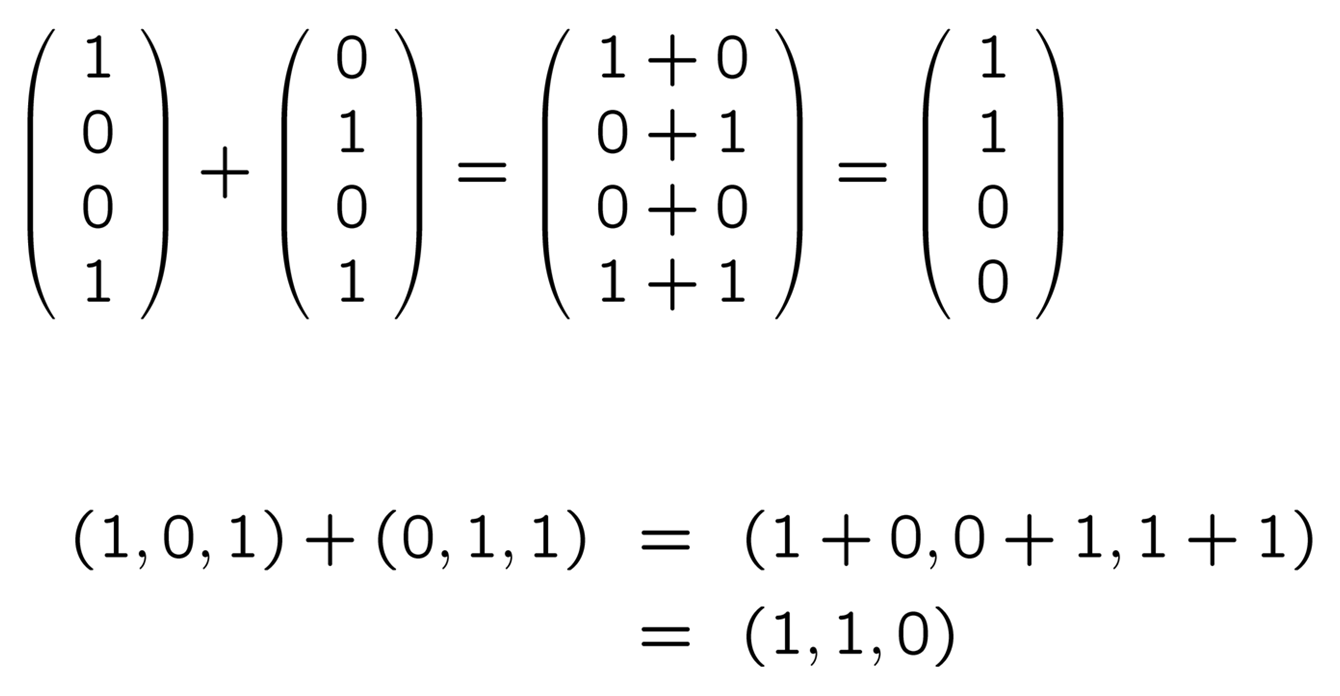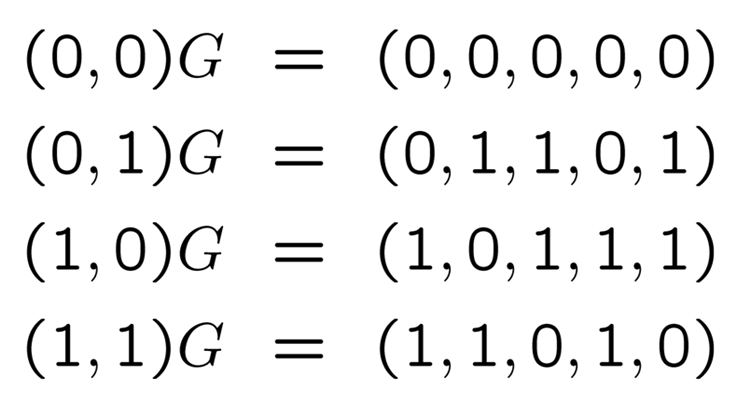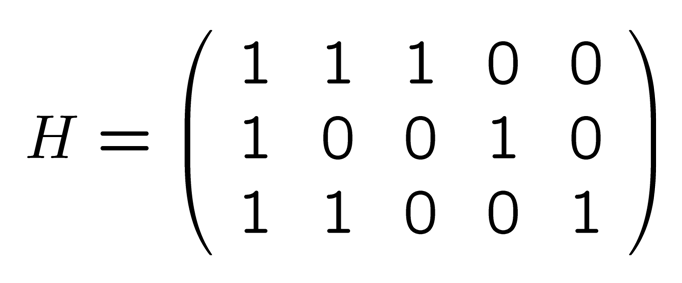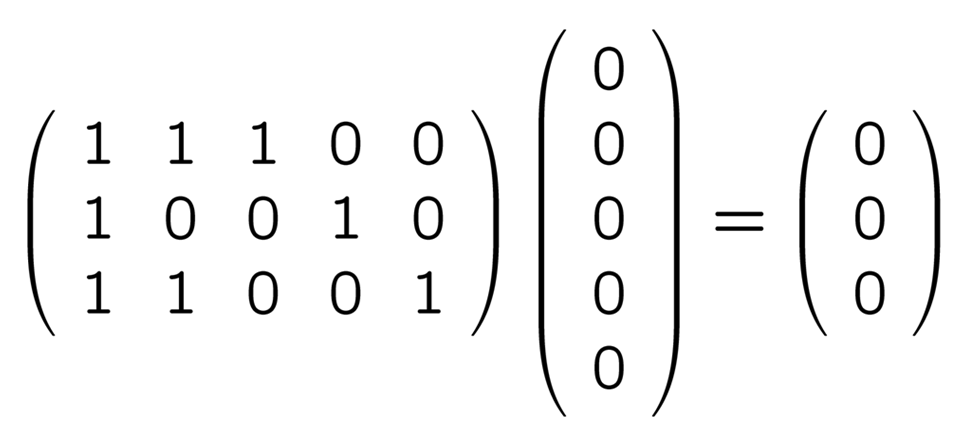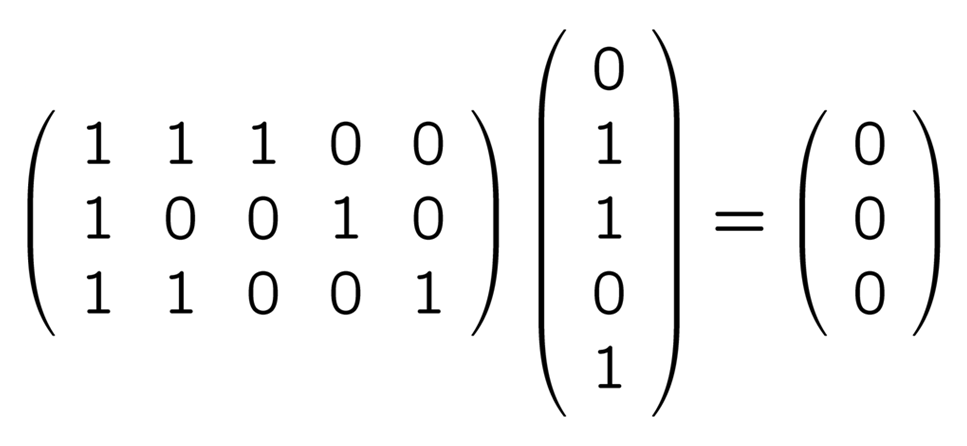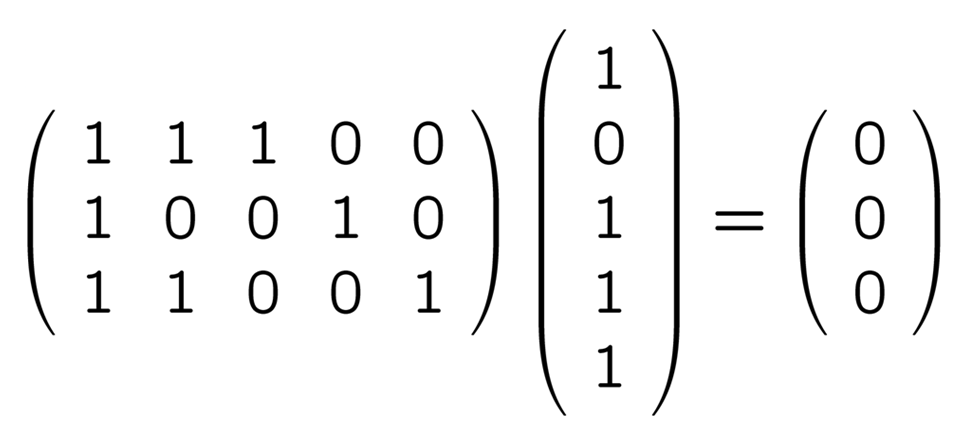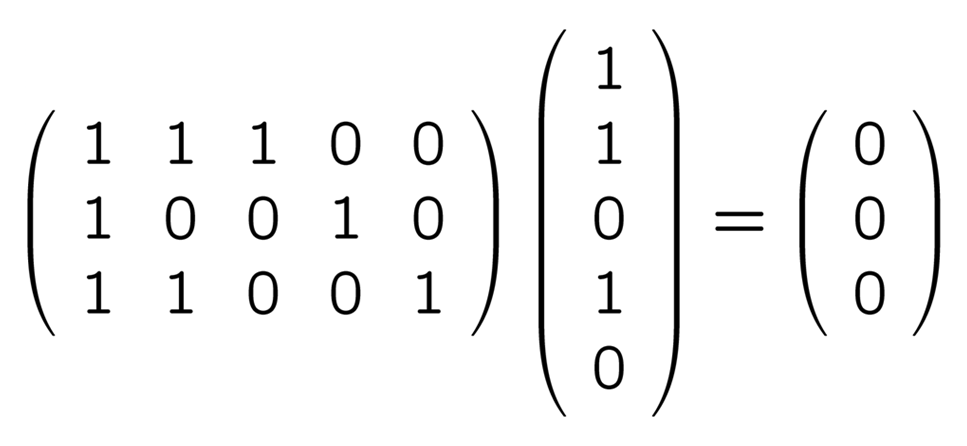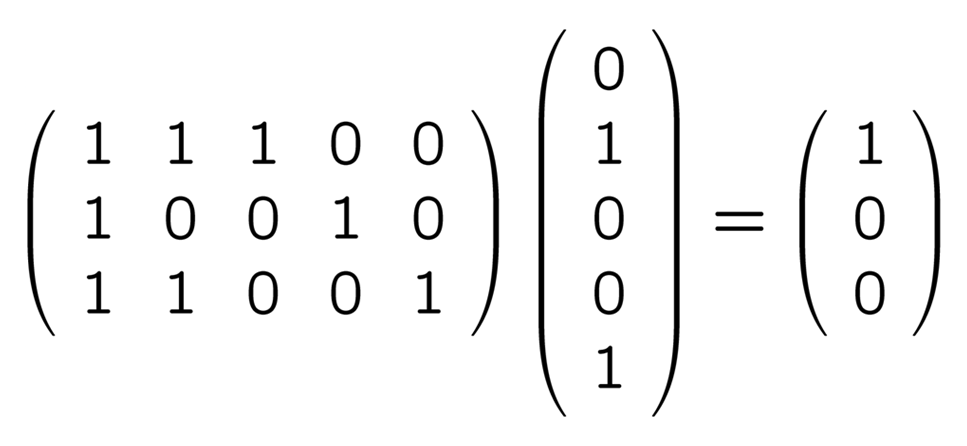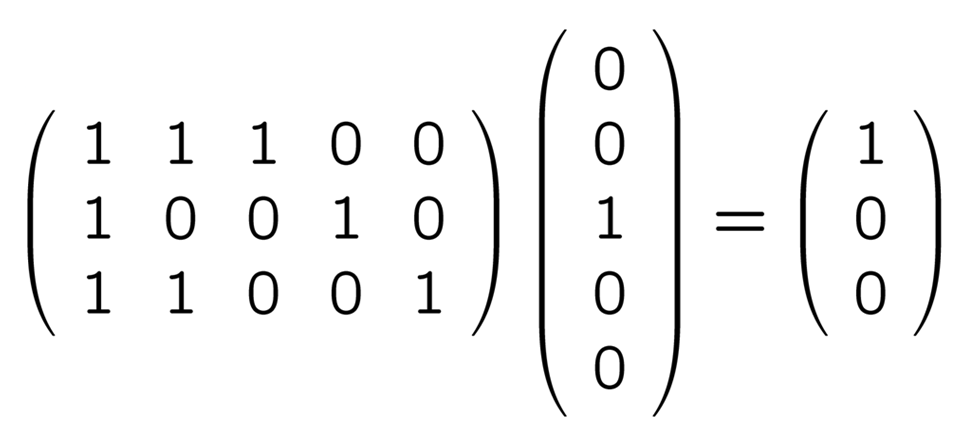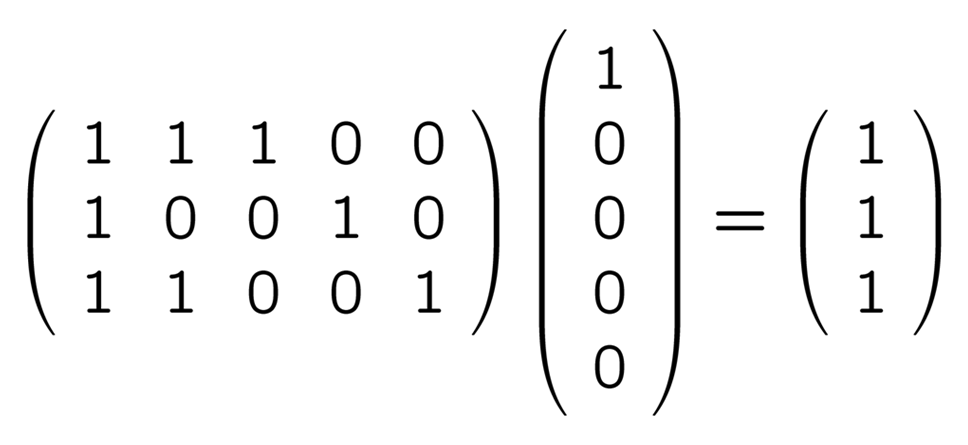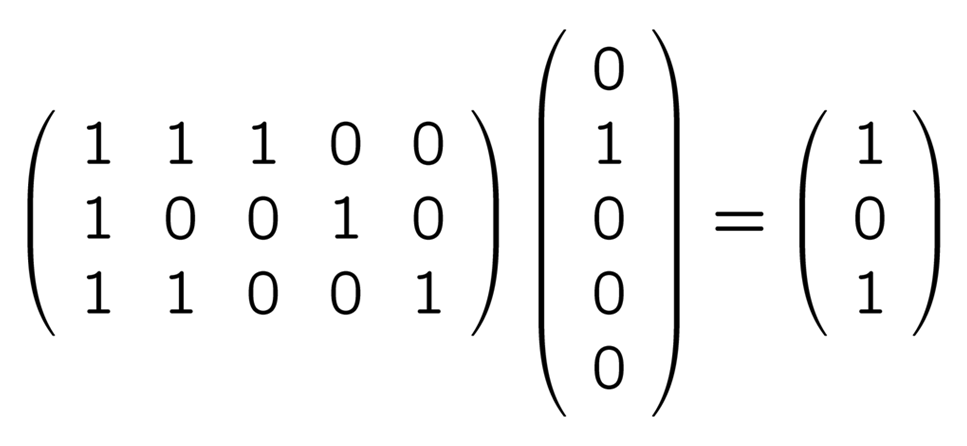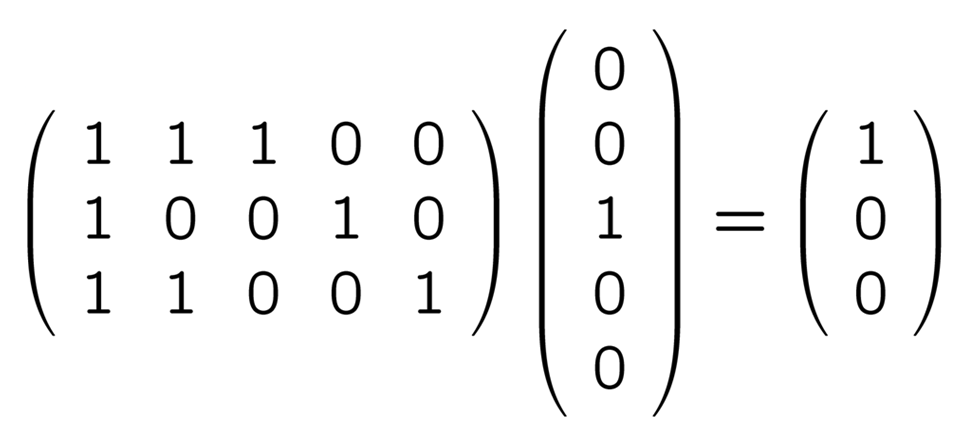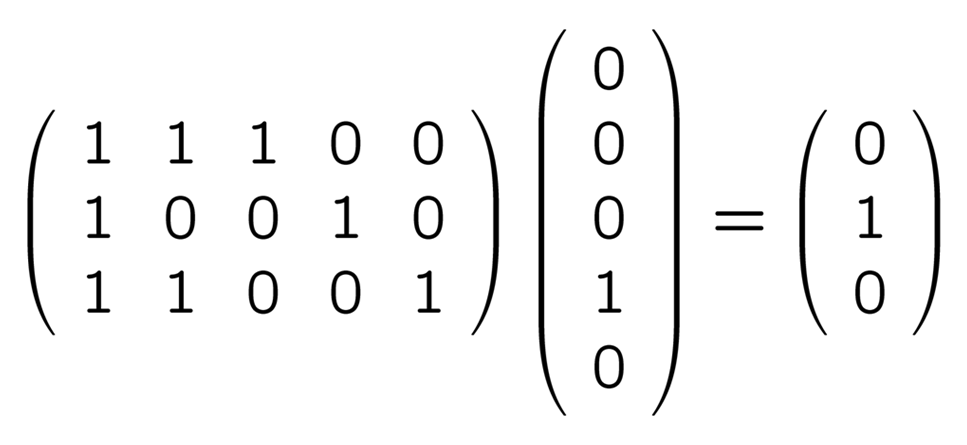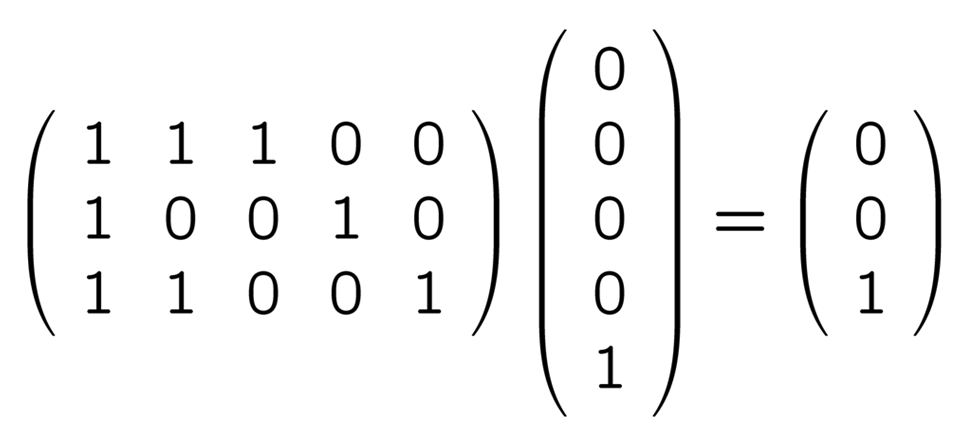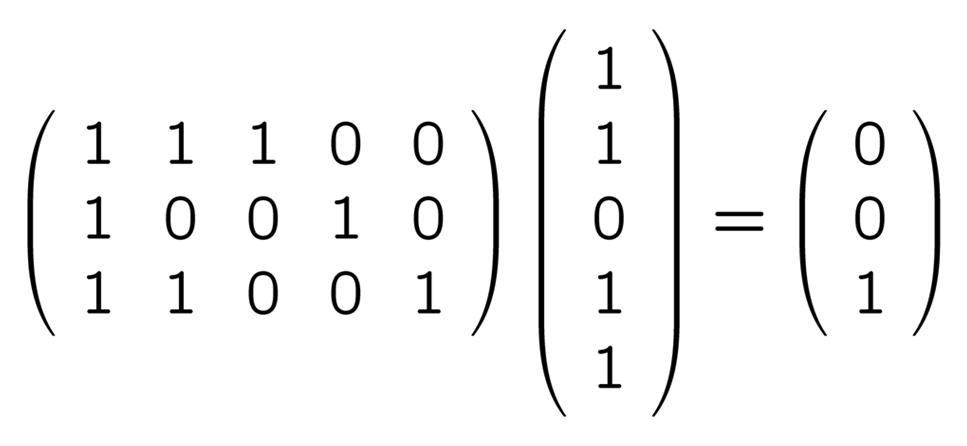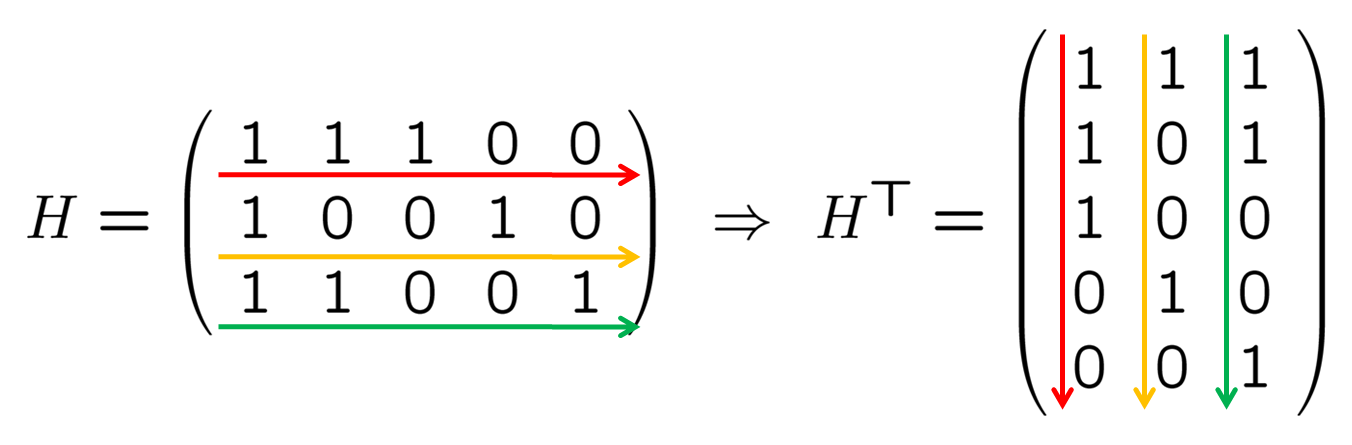誤り訂正符号の実例
実際に誤り訂正が可能な符号を作ってみましょう. 必要なのはベクトルと行列, そして「1+1=0」というちょっと不思議な計算規則です.
1. ベクトルと行列
ベクトルとは, いくつかの数を (横または縦に) 並べて括弧でくくったものです.
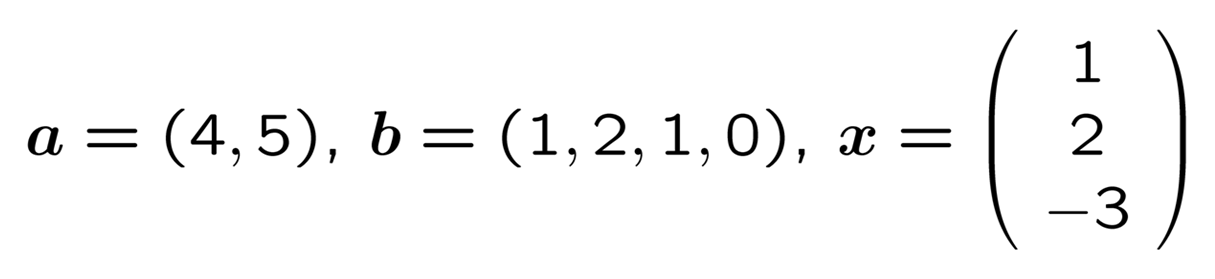
ベクトルの例
横向きにするか縦向きにするかは場合に応じて使い分けます. 2 つの実数が並べられたベクトルは平面上の点を, 3 つの実数が並べられたベクトルは空間の点を指し示すことができます. 4 つ並ぶと「4 次元空間の点」ということになり, われわれの目には見えなくなりますが, それでもちゃんと扱えるところが数学のありがたいところです.
行列とは, いくつかの数を長方形状に並べて括弧でくくったものです.
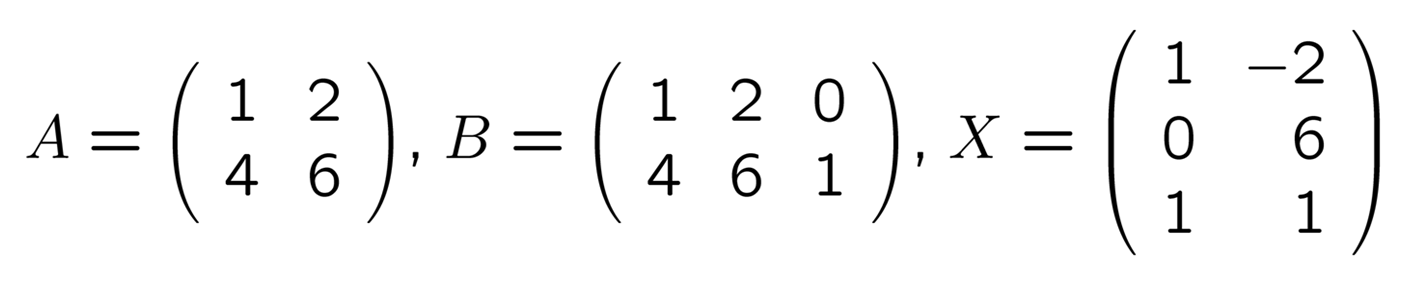
行列の例
ベクトルはボールド体の小文字, 行列は大文字で表すのが普通です. ベクトルを表すのに小文字の上に矢印を書く流儀も多いですが, これは空間や平面で「向きと大きさで決まる量」ということを強調した記号と考えられます. このあとの主題である「情報」も実はベクトルで表すのですが, 情報に矢印をつけるというのは何となく変ですね. そういったこともあり, 大学の数学では「ベクトルはボールド体の小文字」が普通なわけです. また, ベクトルや行列の中に並んでいる数を「成分」といいます.
2. ベクトルと行列の掛け算
このあたりからは紙と鉛筆をご用意頂いた方がいいかも知れません. 一般論は複雑なので, このあと必要な場合だけを述べます.
(1) ベクトル×行列
下の例のように, 横向きのベクトルを前に, そして行列を後ろに置いてこれらを掛けるには, 矢印の向きに数をたどり, 対応する場所にある数どうしを掛けて足し, 順に並べていきます. 結果は横向きのベクトルになります.
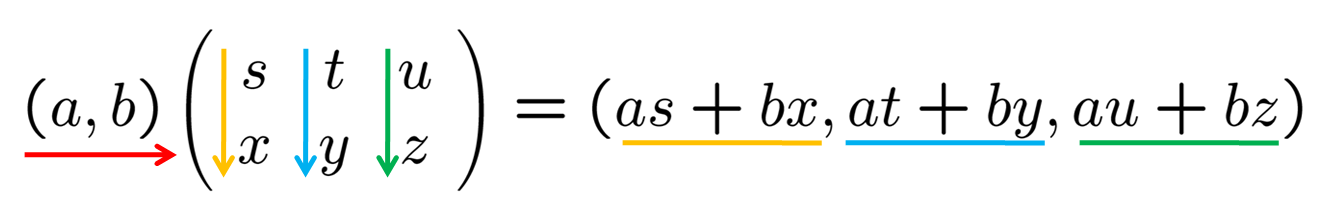
掛け算(1) 前にベクトル, 後ろに行列
したがって, ベクトルの成分の個数と行列の縦の成分の個数が一致するときにのみ掛け算が可能, ということになります.

(2) 行列×ベクトル
今度は前に行列, 後ろに縦向きのベクトルを置きます. 矢印の向きに数をたどり, 対応する場所にある数どうしを掛けて足し, 順に並べていくのは同じです. 結果は縦向きのベクトルになります.

掛け算(2) 前に行列, 後ろにベクトル
行列の横の成分の個数とベクトルの成分の個数が一致するときにのみ掛け算が可能です.
行列どうしの積も条件が合えば可能ですが, ここでは省略します.
3. 情報もベクトルで
実際のディジタル情報はすべて 2 進数の形で扱います. それは, 電流 ON=1, 電流 OFF=0, と電気的に容易に表されるからです. 例えば英文で通信を行うためにアルファベット, その他の記号(ピリオド, コンマ, ハイフンなど, 文字以外にもいろいろ必要ですね)を2進数で表す方法として使われる「ASCII(アスキー)コード」は 7 桁の 2 進数を用いています( 27=128 なので, 128 個のものまでを区別できる, 言い換えれば 128 文字まで 2 進数で扱えます).
誤り訂正のためにもとの情報に余分な情報を付け加える, ということが必要ですが, 実際の符号理論では, それを行列とベクトルの掛け算を利用して行います. そのため, 2 進数で表された情報も, それ自身を 1 つの数として扱うのではなく, 1 桁= 1 つの成分としてベクトルで表します. 次のような感じです:
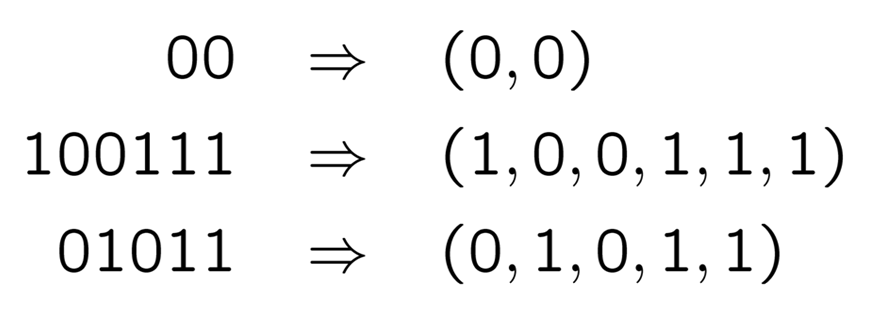
情報もベクトルで
ここで, 一番左の桁が 0 でも, きちんと 0 を書いていることに注意しましょう. 日常扱う数ではこのようなことはしません (「100 円」をわざわざ「00100 円」などとは表わしません). しかし, ベクトルとして扱う以上は, 成分の個数は揃えておく方が数学的には何かと都合がいいので, 何もない桁も 0 で埋めておくのです. したがって, 「これだけの情報を扱うには 7 桁の 2 進数が必要」となればすべて 7 桁に統一しておく, という使い方をします.
4. 1+1=0
小学校以来, 「1+1=2」と習って久しいわけですから, 1+1=0にはちょっと違和感がありますね. あるいは新鮮な感じがする方もあるでしょうか. このように決めると数学的にとてもうまく行く, という数の体系があるのですから不思議です. それは {0,1} という, 0 と 1 のみを要素としてもつ集合で, 実は, この集合の中だけで和, 差, 積, 商をうまく行いたい, という要請から必然的に出てくる計算規則です. 数学者はこの集合を F2 と表します. これは「有限体」と呼ばれるものの一種で, もとは整数論という純粋数学の中から生まれた概念ですが, 今や応用面でもなくてはならないものとなっています. F2= {0,1} での計算規則をまとめると次のようになります:
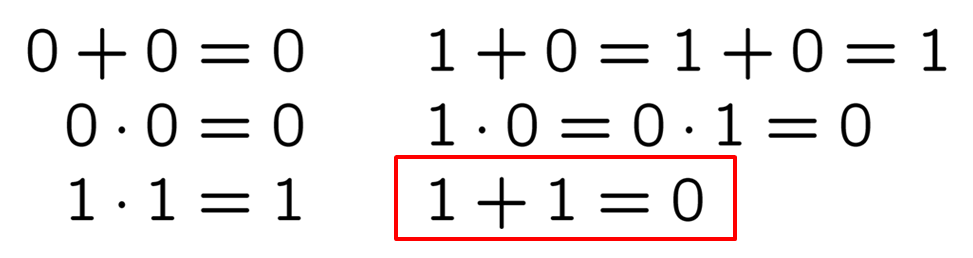
F2 での計算規則
1+1=0以外は普通ですね. ベクトルや行列の計算にもこれを適用します. 2 つのベクトルの和は, 対応する成分どうしを足して, また同じように並べるわけですから, 例えば
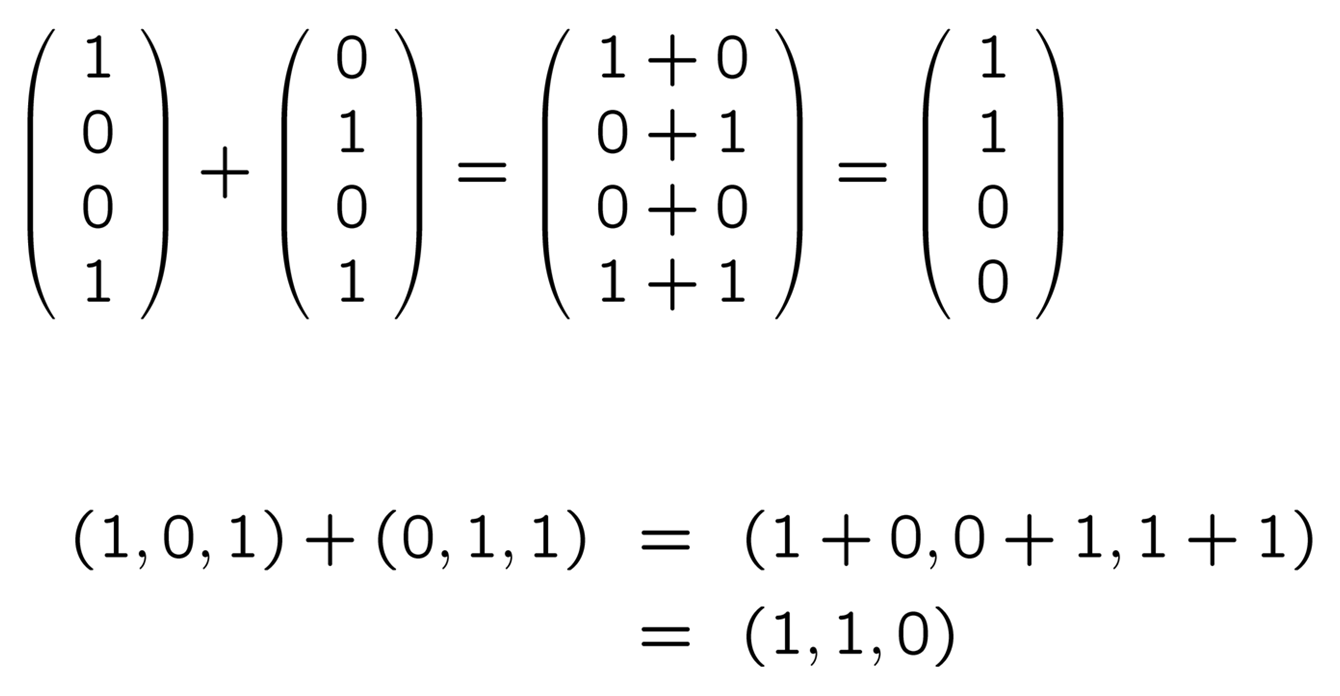
(0, 1 だけの) ベクトルの和
成分の個数が違う 2 つのベクトルを足すこと, 縦ベクトルと横ベクトルを足すことはできません.
5. いよいよ符号化です
伝達途中で誤りが発生しても, それを正しく訂正するためにもとの情報に余分な情報を付け加えること, この過程を「符号化」といいます. 符号化は
もとの情報ベクトルにある行列を掛ける
ということで行います.
さて, もとの情報が 2 桁の 2 進数で表されているとしましょう. つまり 00, 01, 10, 11 の 4つの数, 文字だと 4 文字ですべての文を表現する, という状況です. 現実にはこれでは苦しいですが, 桁数が多いと見づらくて大変ですから, 説明としてはこのくらいがいいでしょう. 余分な情報を付け加える規則を決めることは, 4 つの情報ベクトル (0,0), (0,1), (1,0), (1,1) に(一斉に)掛ける行列を決めることと同じです. ここでは

生成行列 (これを掛ける)
を取ってみます (これには「生成行列」という名前がついています. この取り方によって符号の性能の良し悪しが決まります). なぜこのように取るとうまく直せるかは, 実は少々難しいのですが, 最後に少し触れます. 情報ベクトルとの掛け算の結果は
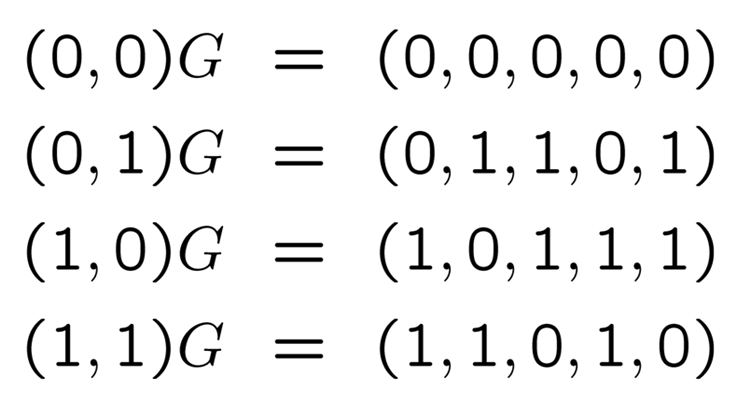
符号化
となります (上に述べた種々の計算規則を使うとこうなります. ぜひ一度ご確認下さい). ちょうど, もとの情報ベクトルの右に余分な桁を 3 桁付け加えたことになっています. 情報の送り手は, この新しくできた長いほうのベクトルを送ることになります. このあと, 例えば (0,1,1,0,1) を 01101 と, わざわざ括弧をつけずに書くこともありますが, 括弧がなくても 2 進数はベクトルとお考え下さい.
6. 誤りの正体
通常の情報伝達では, すべての信号は 0 または 1 のいずれかと解釈されますから, 途中で誤りが発生するということは
0 と 1 が入れ替わること
と表現されます. 例えば 01101 を送ったが 01001 を受け取ったという場合, 真ん中の 1 が途中で 0 に変化した, ということになりますが, ベクトルの和の規則からこの変化は 01101+00100=01001 と表せます. つまりもとのベクトル 01101 に「誤りベクトル」00100 が混入した, ということです. このように, 情報伝達途中での誤り発生がベクトルの和で表せるのです.
7. 誤り訂正
さて, 01001 を受け取ったとき, もともと送られたベクトルが何かを知らない状態で, 送られたベクトルを復元しなければなりません. それには別の行列
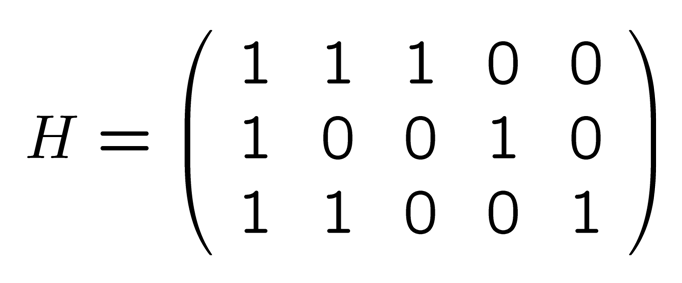
パリティ検査行列 (誤り訂正に使う)
を用意します (「パリティ検査行列」という名前がついています). まず, もともと送られるベクトルは
00000, 01101, 10111, 11010
の 4 つです. これらを縦ベクトルにして, 上の H と掛けてみましょう. まず
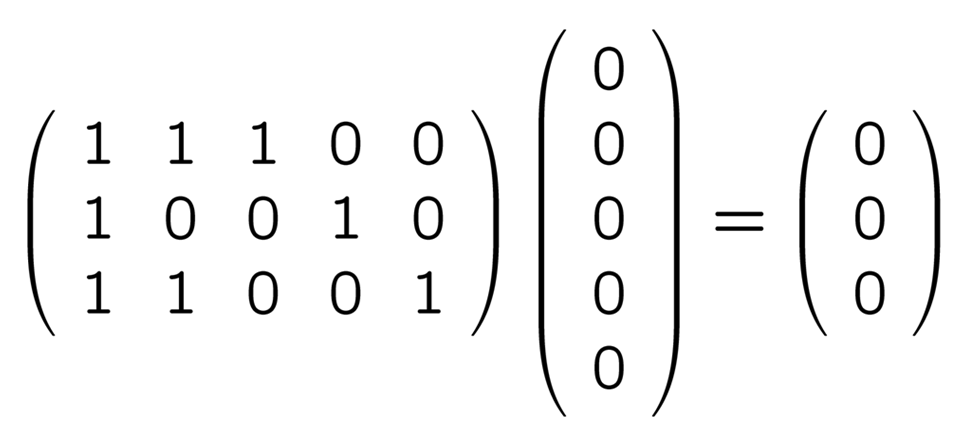
は簡単ですが, 他のベクトルで試してみても
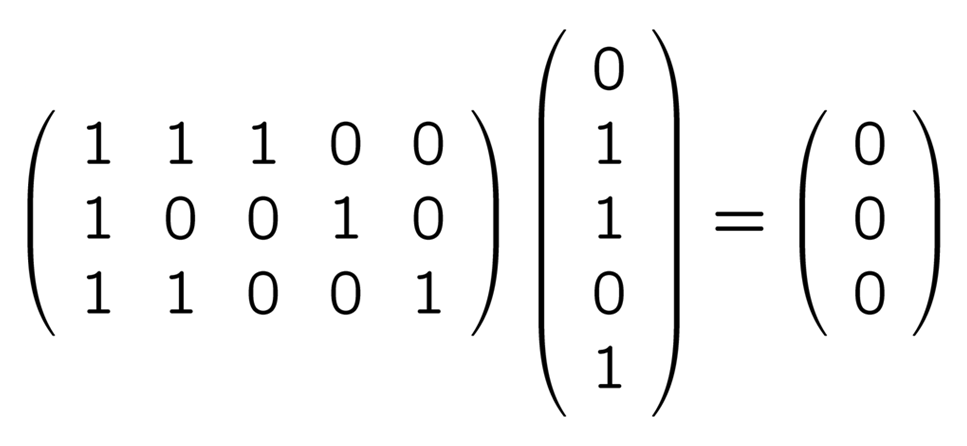
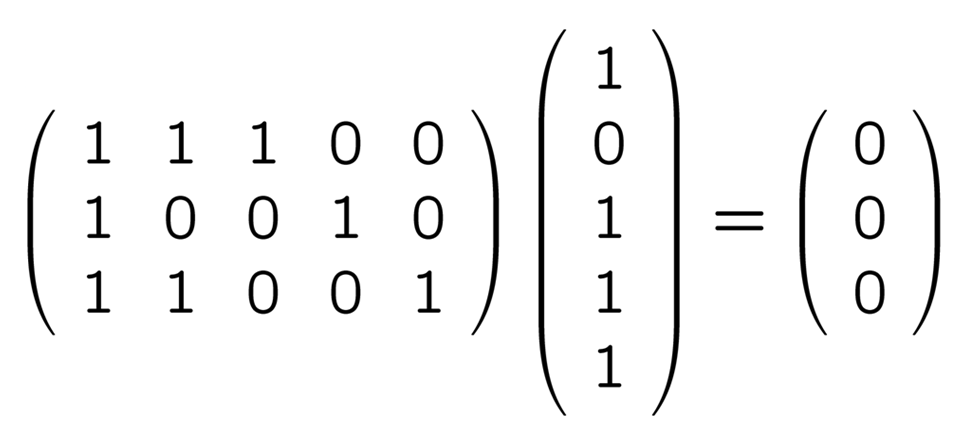
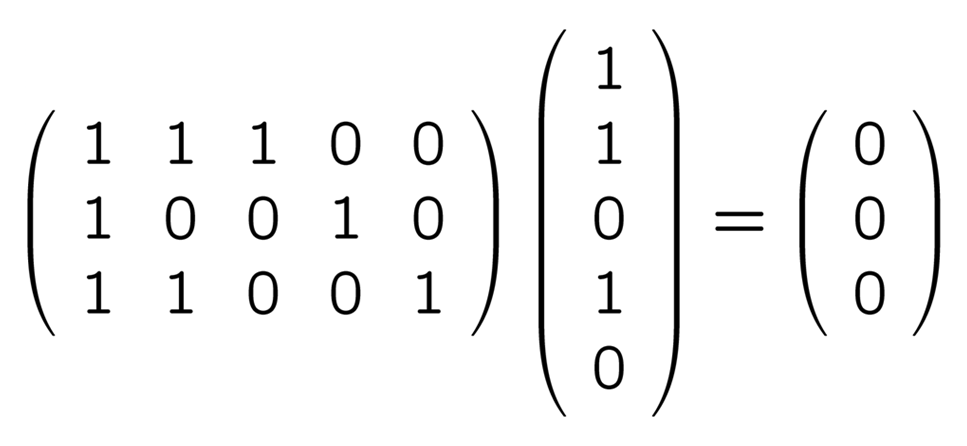
という風に, いずれも 0 ばかりが並んだベクトル (「零ベクトル」といいます) になります. というわけで
H と掛けて零ベクトルになれば誤りは発生しなかった
と考えていいでしょう. では, 誤りを 1 つ含む, 例えば 01001 を縦にして H と掛けるとどうでしょうか:
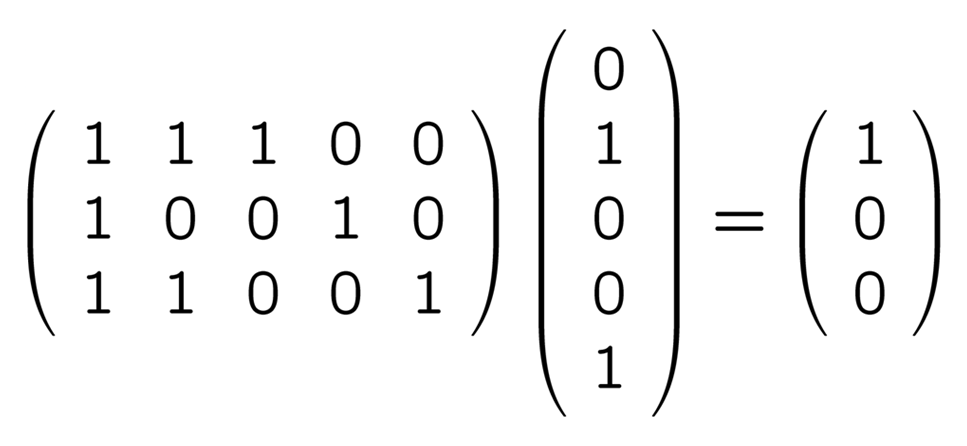
確かに, 零ベクトルでないベクトルが現れました ! そこで
H と掛けて零ベクトルでないベクトルが出れば, 誤りが発生したと判断する
と考えてよさそうです. ところで, 01001 は 01101 に誤りベクトル 00100 が混入したものでした. そこで 00100 に対して同じ計算をすると
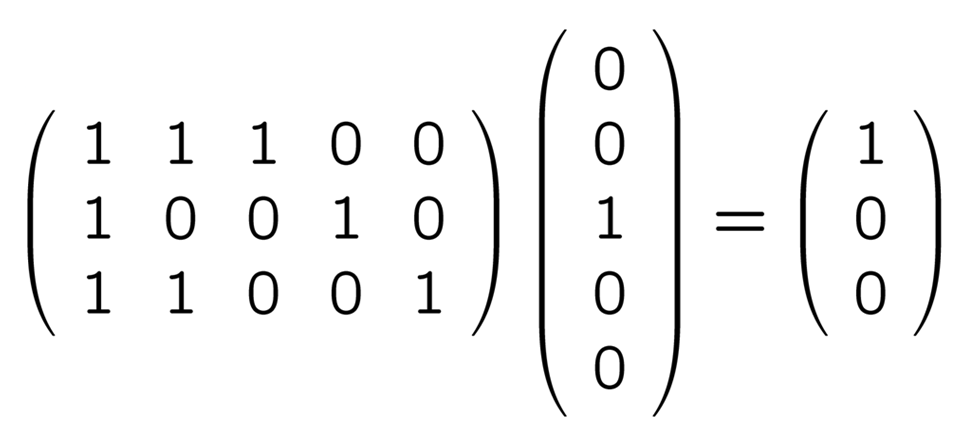
さらに, 5 桁のうち 1 桁に誤りが混入する, という場合には 5 通りあります. つまり, 誤りベクトルには
10000, 01000, 00100, 00010, 00001
の 5 つがあるということです. これらと H との積は順に
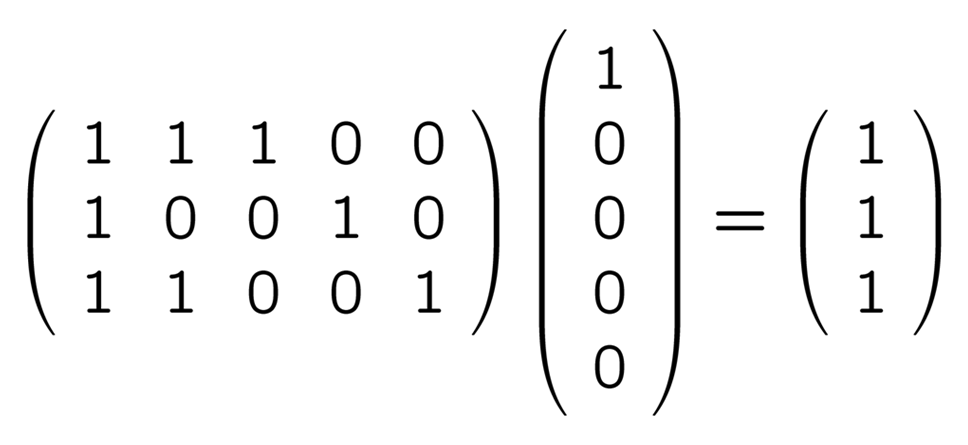
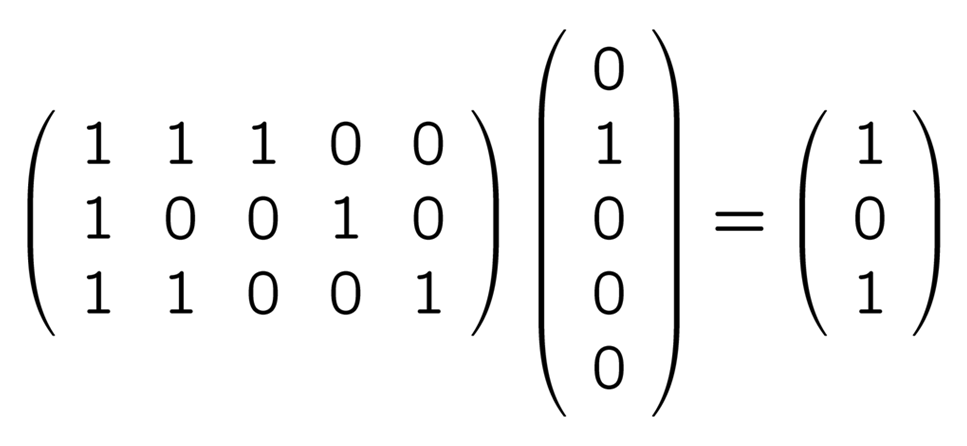
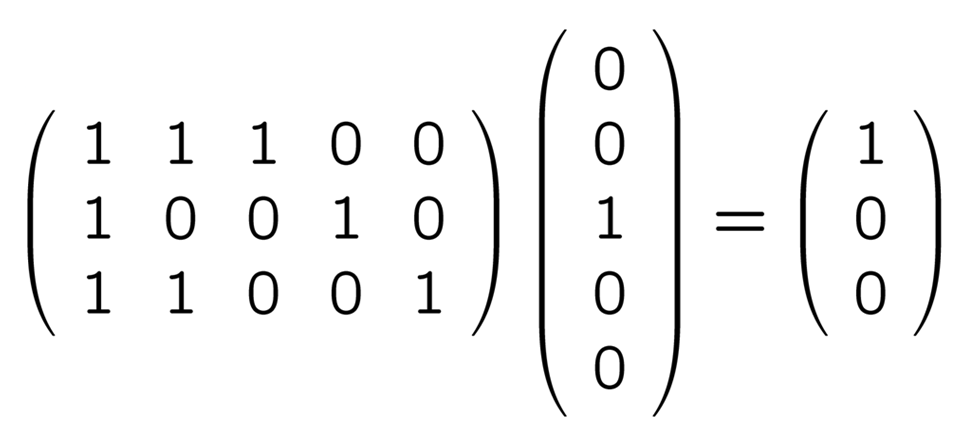
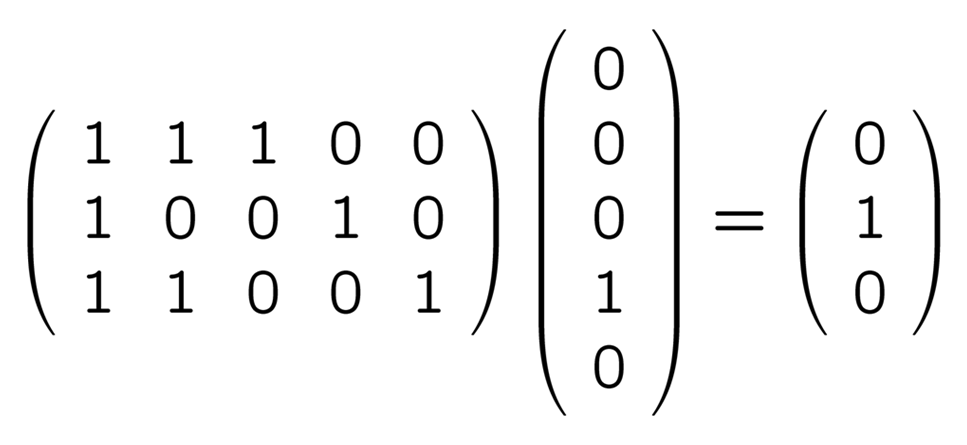
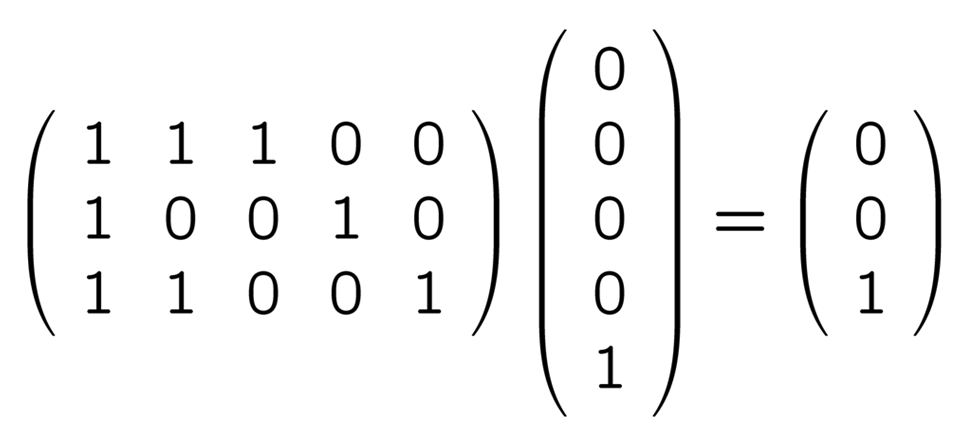
誤りのパターンと H との積
つまり誤りの位置によって, H と掛けて出てくるベクトルが違うということです. 正しい送信語 00000, 01101, 10111, 11010 に誤りベクトルが混入したものでやってみても同じ結果になります (難しい言葉で言えば
「線型性」が効いています).
結局, 誤りの訂正は次のようにすることになります:
1. 受け取ったベクトルと H を掛ける.
2-a. それが零ベクトルなら誤りなしと判定.
2-b-1. それが零ベクトルでないなら上の「誤りのパターンと H との積」で誤りの位置を特定.
2-b-2. 受け取ったベクトルから誤りベクトルを引く (それが正しい情報).
例. 11011 を受け取ったとき.
縦に並べて H と掛けると
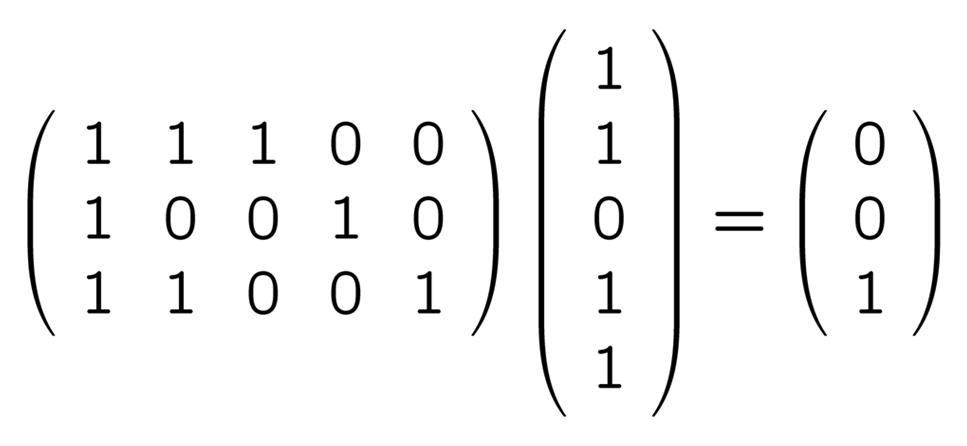
これは 00001 を縦に並べて H と掛けたものと同じだから, 誤りは 00001 だと判定,
11011−00001=11010
が本来送られてきたベクトルと判断する.
8. 最後に
まず少し疑問が残るところは, もっと多くの誤りが起きたらどうなるか, という点です. 結論からいうと「訂正不可能」となります. つまり, この G, H の取り方では, 5 桁につき 1 個の誤りにしか対応できません (試しに 2 箇所の 0, 1 を入れ替えたベクトル, 例えば 11010+01100=10110 を縦向けて H と掛けてみて下さい). もっとたくさんの誤りにも対応したいなら, より「性能のいい行列」を探す, ということになります.
上のような行列 G, H をどうやって決めるか, という問題ですが, きちんとやるのは案外難しく, 特に「何桁増やせばいくつの誤りまで対応できるか」(上の G, H は縦の列が 5 個ありますが, なぜ 5 個か) まで考えると, これは専門的な符号理論で学ぶ内容になってしまいます. また, 実際に「究極のよい行列」を見つけることは, 最先端の符号理論にとっても非常に難しい問題に属します (だからこそ符号理論は研究され続けているのです).
ただ, 本稿の例の G, H は次のような考え方で作りました: まず H は, 誤りベクトルの種類によって, 掛けた時に違うベクトルが出ればよいのですから, 5 つある H の列 (縦の並び) がすべて異なるように作りました. 次に G は
GHT=O
となるようにすればよいことが知られています. ここで HT は H の転置行列と呼ばれ, H の横の並びをすべて縦に並べかえて作った行列, O は零行列 (すべての成分が 0 の行列) です. なお, 通常の数学では転置行列を左肩に t をつけて表します ( tH ) が, 符号理論では右肩に T をつける流儀が普通です (恐らくその方が都合のいい場面が多いからでしょう).
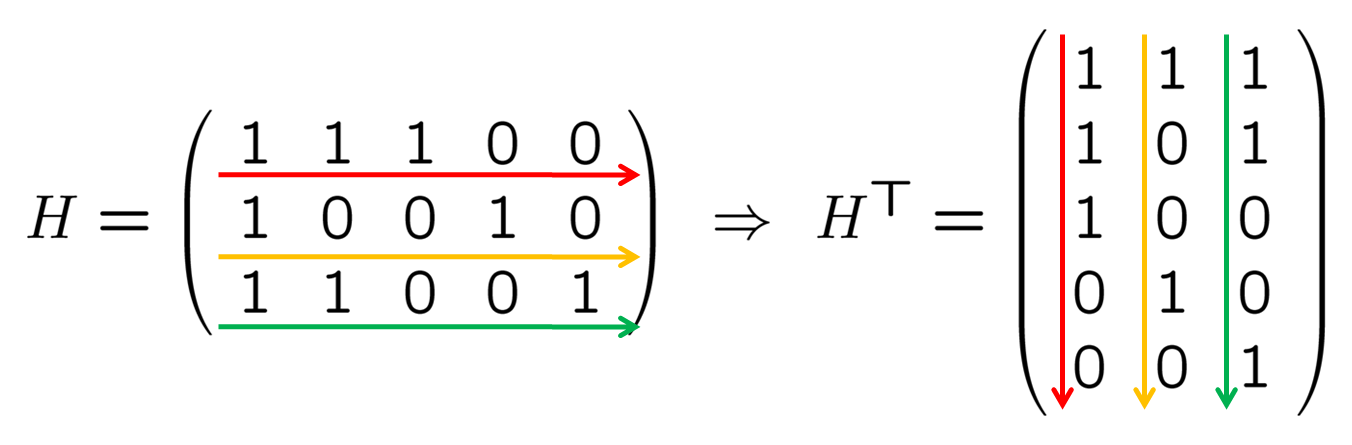
転置行列
さらに種明かしをすると, 上の H は右側に単位行列ができていて, この場合, G は次のような簡単な操作で作ることができます:
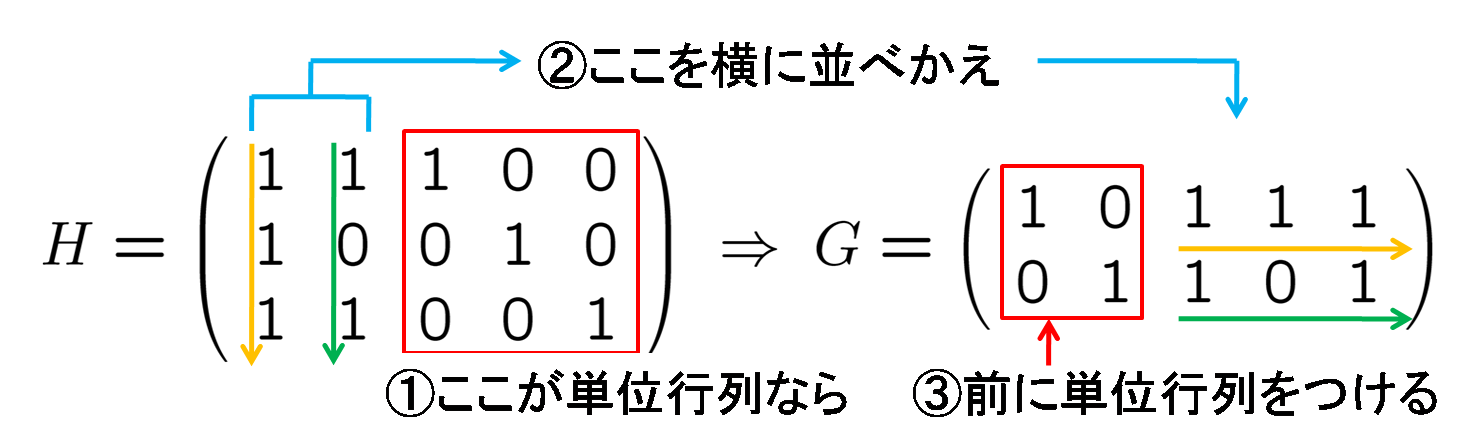
この G, H に対して GHT=O が成り立つことは直接確かめられます. 一般的に証明することは大学で学ぶ「線型代数学」の内容となります.
符号理論は大学 1 年で学ぶ「線型代数学」の, さらにその先にある分野です. 高校数学は, こうした先端技術を支える学問の, 出発点にもなっています.
2008.3 公開, 2019.7 改訂
応用代数学研究室に戻る