誤り訂正の考え方

ここでは誤り訂正符号というものがなぜ必要か, どんな風に働くかを簡単に説明してみたいと思います.

1. アナログとディジタル

「アナログ」と「ディジタル」という言葉は相反する意味の言葉として, 対比して使われますが, 今はディジタル全盛の時代. 音楽でも昔のLPレコードやカセットテープを知る人は, 今後ますます少なくなっていくことでしょう. ここでは音楽をCD (コンパクト・ディスク) に記録すること (PCM方式) を考えましょう. 音は空気の振動が伝わっていくものですが, これを電気的に記録するには, 時間の経過に伴う振動の変化の様子を, 電気信号の変化に直せばよいでしょう. いま, 時刻と電圧の対応が次のようなグラフとして得られたとします:

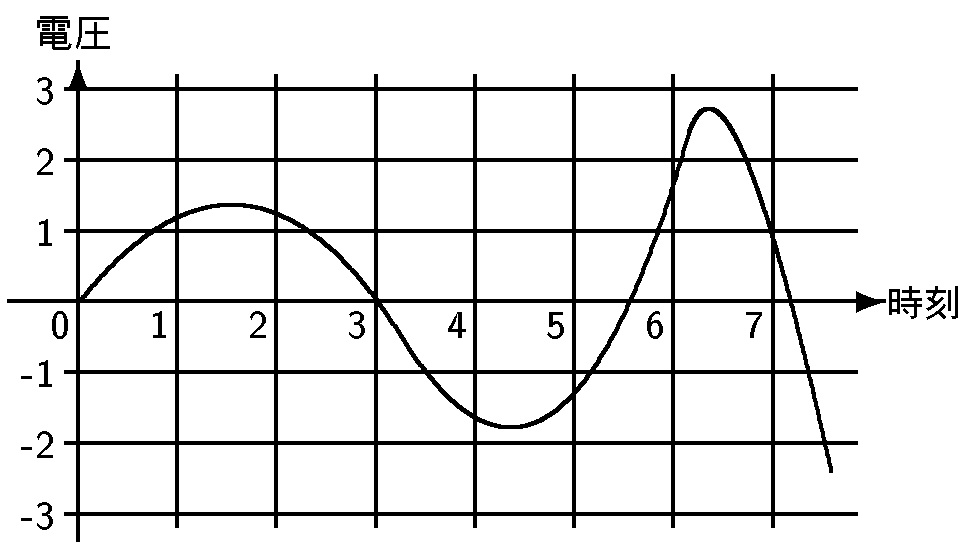
こうしたグラフ (曲線) は一種の図形であるわけですが, これを言わば「図形のままで」記録するのがアナログ方式です. つまり, このグラフの曲線を, 一定の規則に基づいて縮小し, 円板上に刻んでいくと1枚のLPレコードが出来上がる, といった感じです.

2. ディジタル情報は「数の表」

時刻 電圧
0 0.0
1 1.2
2 1.2
3 0.0
4 -1.7
5 -1.3
6 1.6
7 0.9
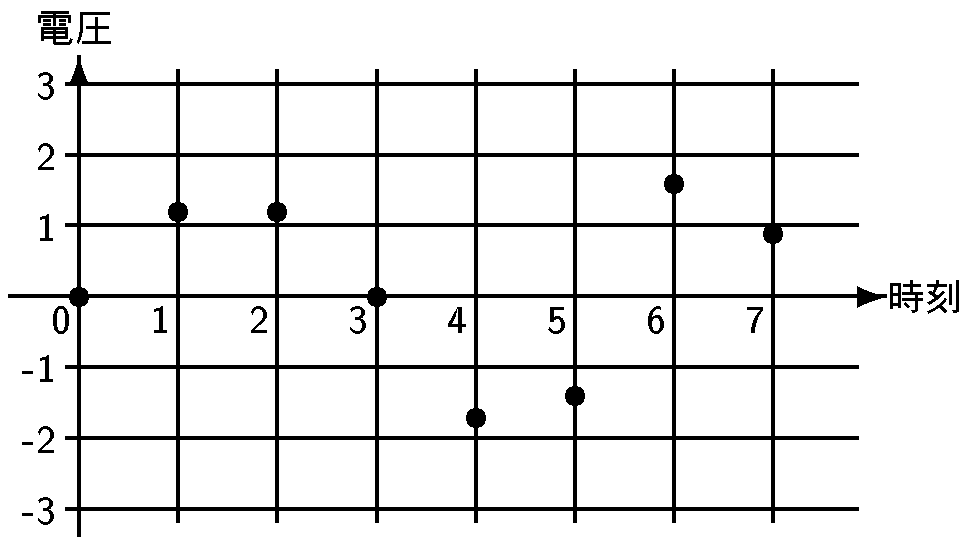
　しかし, ディジタル方式の記録は全く違う発想によります. まずは上のグラフから, 各時刻 0, 1, 2, ... のときの電圧値を目分量でいいですから読み取ってみましょう. 大体右のようになるはずです.
ディジタル方式で記録する, というのは, まさに右のような数表を記録しておくことなのです. 再生するにはどうするかというと, この数表を機械に読み取らせて, 各時刻に数表にある通りの電圧を発生させてスピーカーに送ればよい, ということになります. 次のような感じです:


時刻 電圧 時刻 電圧
0.0 0.0 4.0 -1.7
0.5 0.7 4.5 -1.8
1.0 1.2 5.0 -1.3
1.5 1.4 5.5 -0.3
2.0 1.2 6.0 1.6
2.5 0.8 6.5 2.6
3.0 0.0 7.0 0.9
3.5 -1.0 7.5 -2.0
あれっ?, と思いますね. もとの滑らかなグラフとは似ても似つかない, 飛び飛びのグラフです. 電圧を測った時刻がもともと飛び飛びなのですから, これは仕方ありません. でも, 電圧を測るタイミングをもっと増やしてマス目を細かくすれば, 本来のグラフに近くなるのではないでしょうか. 例えば右のように測る回数を2倍にすると,



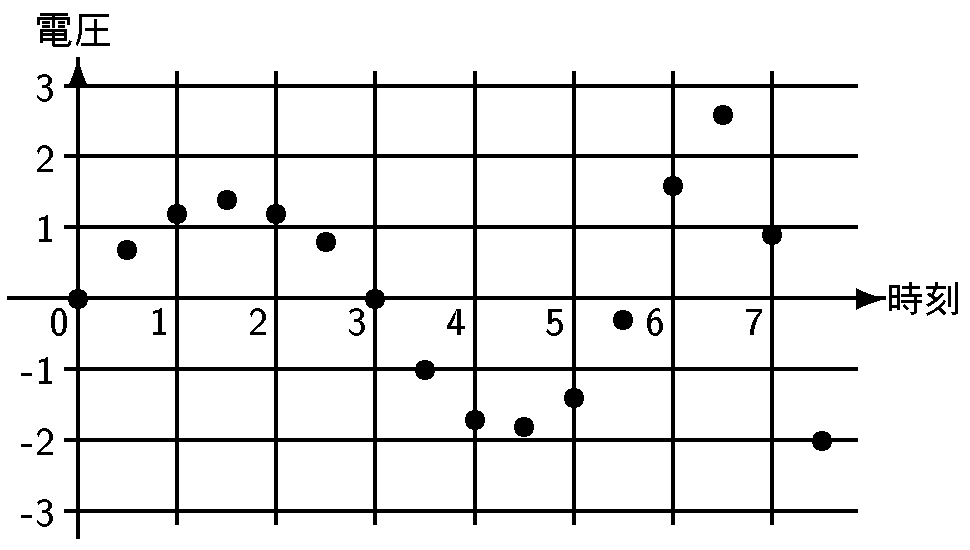
これで元の波形に多少は近づきました. 測る回数をもっと増やせば, もとの曲線とほぼ見分けがつかなくなっていくと予想されます. これに関して, 次の 2 つのキーワードがあります: CD 方式の場合, 標本化周波数は 44.1 kHz (1 秒間に 44100 回, 音を測る), 量子化ビット数は 16 ビット (「音の強さ」(というか, 測定すべき信号値の範囲) を 216=65536 段階に分けて測る) となっています. CD に記録されている音楽, それだけでなく, ディジタル方式で記録された情報はすべて, 音や図形そのものではなく, このような「数表」なのです.

　さて, アナログ録音とディジタル録音の違いとして, アナログ方式は複製を繰り返すと音質が劣化するが, ディジタル方式ではそうしたことは起こらない, ということをよく耳にします. それは上のような記録の原理の違いを見れば納得できます. つまり, アナログだと波形をそのまま図形としてコピーするため, 何回もコピーしていると次第にゆがんできて, もとの波形と厳密には一致しなくなります. これが音の歪みとなって現れてきます. 一方, ディジタル方式では, すべて数値で記録しているため, コピーで文字が薄くなったり, 汚れがついたりしても, 数値さえ間違いなく読み取れれば, つねに正しく再生できる, というわけです.
　また一方, CDではあまり高い周波数の音は記録されないが, レコードにはかなり高い周波数の音まで記録できる, という話もあります. これは, 上で説明した PCM 方式だと, 音を測る回数を無限に大きくできないために起こることです. 測る回数よりも速いペースで振動する音を記録できないのは当然のことなのです. CD には大体 20 kHz までの音が記録できるとされていますが, これは標本化周波数の半分弱, というところです.

英語の digital は digit という語の形容詞で, digit は本来「指」という意味 (フランス語の doigt (指) も同系統の語). 指で物を数えるところから「数字」という意味も派生しました. 「ディジタル方式」というのは, まさに「数字で記録する」という意味合いを持っているのです.
3. 誤り訂正の必要性

　ディジタル方式では, 数値さえ間違いなく読み取れればよい, と述べましたが, この「間違い」が, 実際には起こるのです. CD を再生することを考えると, ディスクにゴミがついていたり, 傷があったりして, 記録された情報を正しく読み出せないこともあり得ます. また, 正しく読み出せても外部から電気的なノイズが入って情報が書き換わってしまうことも考えられます. そしてディジタル情報においては, たった 1 文字書き換わっただけでも重大な結果になってしまいます. 最初のグラフで, 時刻 4 のときの値 -1.7 を 1.7 と読み違ったとすると, 次のような, 全く違う波形になってしまうでしょう:


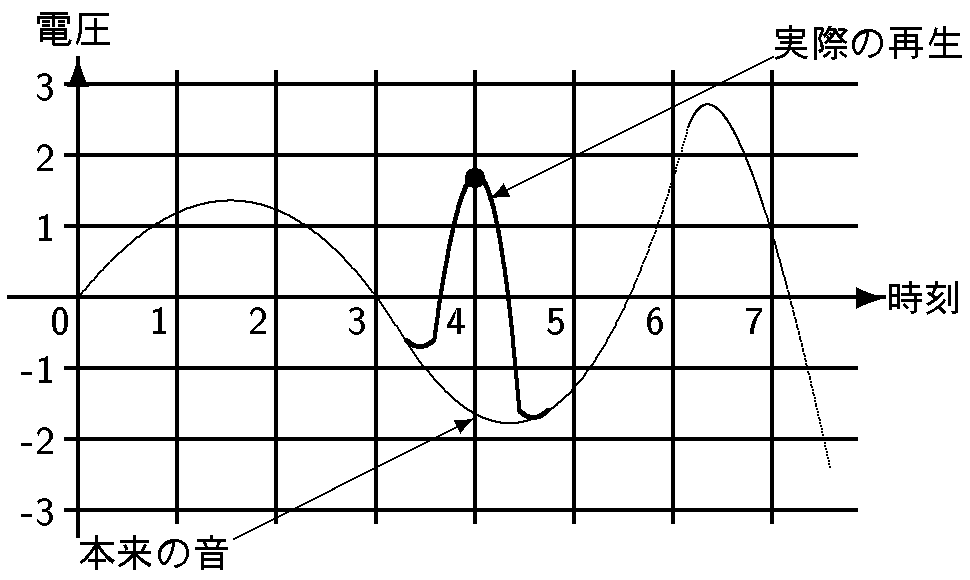
そこで, こうした誤りは, ぜひとも防ぐ必要があります.

4. 訂正の原理 ---「虫食い算」の発想

　何もしないで間違った情報を元に戻す, 魔法のような方法はなく, あらかじめ情報に「仕掛け」をしておく必要があります. 音楽 CD から少し離れて, 次の状況を考えます: カードに数字を書いて誰かに送るとします. しかし, 送られる途中で汚れがついて, 1文字消えてしまうとしましょう.

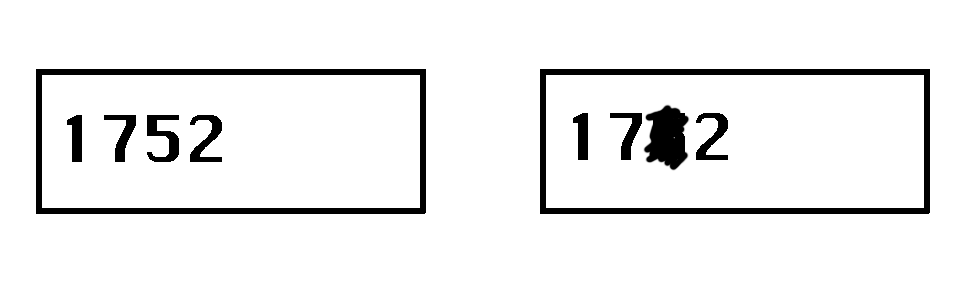このままでは受け取った人が消えてしまった数を復元することはできませんが, ちょっと余白があるのを利用して, 各数の和 1+7+5+2=15 を書き加えて送りましょう:

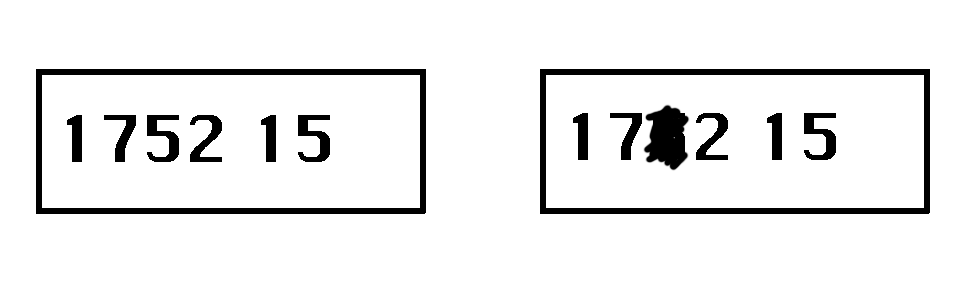すると消えてしまった数は 15-(1+7+2)=5 と復元できます. このように, 余分な情報を少し付け加えておけば, どこかが読めなくなっても復元できるというのが, 基本的な考え方です.
　もっと余白があれば, 例えば 1+2・7+3・5+4・2=38 (つまり 4 桁の数 a, b, c, d に対して a+2b+3c+4d を作る) をさらに書き足しておきましょう. すると, 2 つの数が読めなくなっても復元できることがわかります:

この場合,
a+7+c+2=15
a+2・7+3c+4・2=38
を連立させて解けば, a=1, c=5 と復元できます.
　このように, 余分に付け加える情報が多ければ, たくさんの個所で誤りが起こっても訂正できるようになります. しかし, こうして付け加えた情報は本来は必要のないものなので, あまり多く付け加えると情報伝達の効率は落ちます (上の例でも, 本来伝えたいのは 1752 の 4 桁. しかし 2 個所の誤りに対応するため 1752 15 38 と, 計 8 桁も送った). そこで, 付け加える情報がなるべく少なくて済み, なおかつ訂正能力が高い仕組みを考案することが望まれ, ここに符号理論研究の一つの意義があるのです.

　実際のディジタル情報はすべて 2 進数 (0 と 1 だけですべての数を表現する) の形で扱います. また, 使われる数学は行列, ベクトル, 連立 1 次方程式の, より進んだ理論です. そうした厳密な理論は, ぜひ大学で学ばれることをお勧めしますが, 次のリンク (★印) では最も簡単な場合を解説しています. 興味のある方はぜひご覧下さい.

★誤り検出符号の実例
★誤り訂正符号の実例

2007.4 公開, 2008.3 改訂

応用代数学研究室に戻る