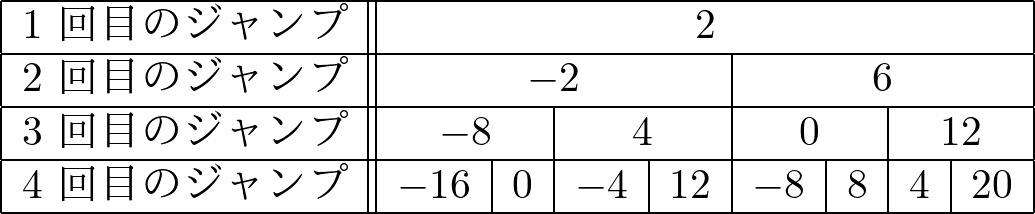レニングラード数学オリンピアード

$23$ 人の生徒の年齢は $10, 11, 12, 13$ 歳のいずれかであり，各年齢の生徒は $1$ 人以上いる．彼らの年齢の合計は $x$ 歳である．もし $12$ 歳の生徒数が $13$ 歳の生徒数の $1.5$ 倍ならば，$12$ 歳の生徒は何人いるだろうか？

各桁が異なる $7$ 桁の数で，各桁の数で割り切れるものをすべて列挙せよ．

バッタはまず初めに $2\mathrm{cm}$ 飛ぶ．それから，同じ向きか逆向きに $4\mathrm{cm}$ 飛ぶ．そして，同じ向きか逆向きに $6\mathrm{cm}$ 飛ぶ．これを（$8\mathrm{cm},10\mathrm{cm},\ldots$ と）繰り返す．下記のような $n$ 回目のジャンプまでの表を作成せよ．

「$n$ 年にナターシャの歳は，彼女が生まれた年の各桁の和と等しくなった．ただし，$n$ は $3$ 桁とする．彼女の生まれた年は何年か？」という問題が解を持つ $n$ をすべて求めよ．

$k$ を $2$ から $9$ までの整数とする．$0$ から $9$ までの数が $1$ つずつ書かれた $10$ 枚のカードがある．$2$ 桁以上 $4$ 桁以下の $k$ の倍数を常に作ることができるカードの最小枚数はいくつか？

立方体の頂点に $1, 2, 3, \ldots, 8$ のラベルを付けて，$6$ つの各面の $4$ つの頂点のラベルの和が同じになるようなラベル付けをすべて列挙せよ．

ヒント：正六面体群について調べよ．

$1$ から $n$ までの番号が書かれたカードが $2$ 枚ずつある．同じ番号のカードの間にはその番号の示す枚数のカードが並ぶように並べる並べ方が何通りあるか．できるだけ大きい $n$ に対して求めてみよう．

総当たり戦において，$6$ 人の各参加者は自身以外の参加者全員とちょうど $1$ 回ずつ対戦する．参加者は勝つと $1$ 点を，引き分けると $0$ 点を，負けると $-1$ 点を得る．総当たり戦が終わったとき，参加者の $1$ 人が $1$ 点で，別の $1$ 人が $4$ 点である総当たり戦をすべて構成せよ．

引き分けのない総当たり戦において，どの $2$ チームもちょうど $1$ 回試合を行った．参加チームを $1$ 列に並べて，各チームがその列における次のチームに勝っているようにするプログラムを作成せよ．

総当たり戦において，どの $3$ チーム $\mathrm{A}$，$\mathrm{B}$，$\mathrm{C}$ に対しても，「$\mathrm{A}$ が $\mathrm{B}$ に勝ち，$\mathrm{B}$ が $\mathrm{C}$ に勝っているならば，$\mathrm{A}$ が $\mathrm{C}$ に必ず勝っている」とき，その総当たり戦は推移的であるという．$n$ チームの引き分けのない総当たり戦が与えられたとき，推移的である $\lfloor \log_{2}n \rfloor +1$ チームだけの総当たり戦を求めるプログラムを作成せよ．